In engineering, we often deal with the idea of an action occurring at a point. Whether it be a force at a point in space or a signal at a point in time, it becomes worth while to develop some way of quantitatively defining this. This leads us to the idea of a unit impulse, probably the second most important function, next to the complex exponential in systems and signals course.
Dirac Delta Function:
The Dirac Delta function, often referred to as the unit impulse or delta function is the function that defines the idea of a unit impulse. This function is one that is infinitesimally narrow, infinitely tall, yet integrates to unity, one. Perhaps the simplest way to visualize this is as a rectangular pulse from a – Є/2 to a + Є /2 with a height of 1/Є. As we take the limit of this,
we see that the width tends to zero and the height tends to infinity as the total area remains constant at one. The impulse function is often written as δ (t).
 |
 |
| Figure 1: This is one way to visualize the Dirac Delta Function. |
 |
| Figure 2 ' |
Figure 2: Since it is quite difficult to draw something that is infinitely tall, we represent the Dirac with an arrow centered at the point it is applied. If we wish to scale it, we may write the value it is scaled by next to the point of the arrow. This is a unit impulse (no scaling).
The Sifting Property of the Impulse:
The first step to understanding what this unit impulse function gives us is to examine what happens when we multiply another function by it.
f(t) δ(t) = f(0) δ(t)………..(1)
Since the impulse function is zero everywhere except the origin, we essentially just "pick off" the value of the function we are multiplying by evaluated at zero.
At first glance this may not appear to give use much, since we already know that the impulse evaluated at zero is infinity, and anything times infinity is infinity. However, what happens if we integrate this?
Sifting Property
 |
| Sifting Property |
It quickly becomes apparent that what we end up with is simply the function evaluated at zero. Had we used δ (t – T) instead of δ(t), we could have "sifted out" f(T). This is what we call the Sifting Property of the Dirac function, which is often used to define the unit impulse.
The Sifting Property is very useful in developing the idea of convolution which is one of the fundamental principles of signal processing. By using convolution and the sifting property we can represent an approximation of any system's output if we know the system's impulse response and input.
Other Impulse Properties:
Below we will briefly list a few of the other properties of the unit impulse without going into detail of their proofs - we will leave that up to you to verify as most are straightforward. Note that these properties hold for continuous and discrete time.
Unit Impulse Properties
 |
| Units Impulse Properties |
Discrete-Time Impulse (Unit Sample):
The extension of the Unit Impulse Function to discrete-time becomes quite trivial. All we really need to realize is that integration in continuous-time equates to summation in discrete-time. Therefore, we are looking for a signal that sums to zero and is zero everywhere except at zero.
Discrete-Time Impulse
 |
 |
| Figure 3 |
Figure 3: The graphical representation of the discrete-time impulse function
Looking at the discrete-time plot of any discrete signal one can notice that all discrete signals are composed of a set of scaled, time-shifted unit samples. If we let the value of a sequence at each integer k be denoted by s [k] and the unit sample delayed that occurs at k to be written as δ[n – K], we can write any signal as the sum of delayed unit samples that are scaled by the signal value, or weighted coefficients.
This decomposition is strictly a property of discrete-time signals and proves to be a very useful property.
The Impulse Response:
The impulse response is exactly what its name implies - the response of an LTI system, such as a filter, when the system's input is the unit impulse (or unit sample). A system can be completed described by its impulse response due to the idea mentioned above that all signals can be represented by a superposition of signals. An impulse response gives an equivalent description of a system as a transfer function, since they are Laplace Transforms of each other.
Notation: Most texts use δ(t) and δ[n] to denote the continuous-time and discrete-time impulse response, respectively.

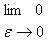
No comments:
Post a Comment